Miscellaneous Topics
Design Patterns
Builder Pattern
When an object has many optional attributes or components, it can be cumbersome to manage constructors with numerous parameters or to manually set properties after object creation.
- The Builder Pattern organizes the construction process into manageable steps.
- With method chaining, the code becomes much more readable and self-explanatory compared to traditional approaches.
Example: A Portfolio
class Portfolio {
private:
double stocks;
double bonds;
double realEstate;
public:
Portfolio() : stocks(0), bonds(0), realEstate(0) {}
void setStocks(double amount) {
stocks = amount;
}
void setBonds(double amount) {
bonds = amount;
}
void setRealEstate(double amount) {
realEstate = amount;
}
void display() const {
std::cout << "Portfolio Contents:\n";
std::cout << "Stocks: $" << stocks << "\n";
std::cout << "Bonds: $" << bonds << "\n";
std::cout << "Real Estate: $" << realEstate << "\n";
}
};In practice, the Portfolio class can have many more attributes like ETFs, mutual funds, cryptocurrencies, commodities, and cash holdings.
Without the Builder pattern, setting up or modifying a portfolio would require either:
- A complex constructor with many parameters
- Multiple setter calls after construction
Portfolio builder
class PortfolioBuilder {
private:
Portfolio portfolio;
public:
PortfolioBuilder& addStocks(double amount) {
portfolio.setStocks(amount);
return *this;
}
PortfolioBuilder& addBonds(double amount) {
portfolio.setBonds(amount);
return *this;
}
PortfolioBuilder& addRealEstate(double amount) {
portfolio.setRealEstate(amount);
return *this;
}
Portfolio build() {
return portfolio;
}
};The use of builder pattern
int main() {
PortfolioBuilder builder;
// Build an aggressive portfolio
Portfolio aggressivePortfolio = builder
.addStocks(10000)
.addBonds(2000)
.addRealEstate(5000)
.build();
std::cout << "Aggressive Portfolio:\n";
aggressivePortfolio.display();
// Build a conservative portfolio
PortfolioBuilder builder2;
Portfolio conservativePortfolio = builder2
.addStocks(3000)
.addBonds(10000)
.addRealEstate(2000)
.build();
std::cout << "\nConservative Portfolio:\n";
conservativePortfolio.display();
return 0;
}Strategy Pattern
The Strategy Pattern is a behavioral design pattern that allows a class’s behavior to be selected at runtime.
- It defines a family of algorithms, encapsulates each algorithm in a separate class, and makes them interchangeable.
- The strategy pattern promotes flexibility, reusability, and the separation of concerns.
- Open/Closed Principle1: The pattern enables adding new strategies without altering existing code, which adheres to the Open/Closed Principle.
Example: A Trading Strategy
In the previous lecture, our logging system was designed as a strategy pattern.
Here we use a new example about a trading strategy. With defining a strategy interface, it’s easy for us to add new payment strategies without modifying the existing code.
#include <iostream>
#include <memory>
#include <string>
// Strategy Interface
class PaymentStrategy {
public:
virtual void pay(int amount) const = 0;
virtual ~PaymentStrategy() = default;
};// Concrete Strategy 1: CreditCard Payment
class CreditCardPayment : public PaymentStrategy {
private:
std::string name;
std::string cardNumber;
public:
CreditCardPayment(const std::string& name, const std::string& cardNumber)
: name(name), cardNumber(cardNumber) {}
void pay(int amount) const override {
std::cout << "Paid $" << amount << " using Credit Card (" << name << ").\n";
}
};
// Concrete Strategy 2: PayPal Payment
class PayPalPayment : public PaymentStrategy {
private:
std::string email;
public:
PayPalPayment(const std::string& email) : email(email) {}
void pay(int amount) const override {
std::cout << "Paid $" << amount << " using PayPal (" << email << ").\n";
}
};
// Concrete Strategy 3: Bitcoin Payment
class BitcoinPayment : public PaymentStrategy {
public:
void pay(int amount) const override {
std::cout << "Paid $" << amount << " using Bitcoin.\n";
}
};Property Injection
class PaymentContext {
private:
std::unique_ptr<PaymentStrategy> strategy;
public:
void setStrategy(std::unique_ptr<PaymentStrategy> newStrategy) {
strategy = std::move(newStrategy);
}
void processPayment(int amount) const {
if (strategy) {
strategy->pay(amount);
} else {
std::cout << "Payment strategy not set.\n";
}
}
};By using property injection, we can inject the strategy object into the PaymentContext object at any time.
int main() {
PaymentContext context;
// Use Credit Card payment
context.setStrategy(std::make_unique<CreditCardPayment>("John Doe", "1234-5678-9101-1121"));
context.processPayment(100);
// Use PayPal payment
context.setStrategy(std::make_unique<PayPalPayment>("john.doe@example.com"));
context.processPayment(200);
// Use Bitcoin payment
context.setStrategy(std::make_unique<BitcoinPayment>());
context.processPayment(300);
return 0;
}Random Number Generation
rand()
The rand() function generates a pseudo-random integer between 0 and RAND_MAX.
int main() {
int num = rand();
for (int i = 0; i < 10; i++) {
std::cout << num << " ";
}
std::cout << std::endl << "RAND_MAX: " << RAND_MAX << std::endl;
return 0;
}rand()will generate a number between 0 andRAND_MAX.- Every time you run the program, you will get the same sequence of random numbers.
srand()
int main() {
srand(time(0));
for (int i = 0; i < 3; i++) {
int num = rand();
std::cout << num << " ";
}
return 0;
}- Like
rand(),srand()generates a number between 0 andRAND_MAX. srand()takes a seed value as an argument, normally we use the current time as the seed value.- If your program runs too fast, you may get the same sequence of random numbers.
std::mt19937
rand()andsrand()can only generate numbers between 0 andRAND_MAX.std::mt19937can generate a much wider range of numbers(2^19937).
#include <iostream>
#include <random>
int main() {
std::mt19937 gen; // default constructor
for (int i = 0; i < 10; i++) {
int num = gen(); // overloaded operator()
std::cout << num << " ";
}
std::cout << std::endl << "min: " << gen.min() << std::endl;
std::cout << "max: " << gen.max() << std::endl;
return 0;
}Generate Random Numbers in a Range
In the previous example, the generated numbers are in the range of [gen.min(), gen.max()].
If we want to generate numbers in a specific range, one simple way is to use the modulo operator.
Suppose we want to generate numbers in the range of [0, 100).
int main() {
std::mt19937 gen; // default constructor
for (int i = 0; i < 10; i++) {
int num = gen() % 100;
std::cout << num << " ";
}
return 0;
}The previous method is not a good way to generate random numbers in a specific range. However, if the devided number is very large, the result will be biased.
C++ provides a better way to generate random numbers in a specific range or with a specific distribution.
std::uniform_int_distribution: generate random numbers in a specific range.std::normal_distribution: generate random numbers with a specific normal distribution.std::uniform_real_distribution: generate random numbers with a specific uniform distribution.
Distribution Generator
int main() {
std::mt19937 gen;
std::uniform_int_distribution<int> dis(1, 6); // int
for (int i = 0; i < 10; i++) {
std::cout << dis(gen) << " ";
}
return 0;
}int main() {
std::mt19937 gen;
std::uniform_real_distribution<double> dis(1, 6); // double
for (int i = 0; i < 10; i++) {
std::cout << dis(gen) << " ";
}
return 0;
}Seed the Generator
The default constructor of std::mt19937 uses the current time as the seed value. It has the same issue as srand().
A better way is to use std::random_device to generate a random seed.
int main() {
std::random_device rd;
std::mt19937 gen(rd());
std::uniform_real_distribution<double> dis(1, 6); // double
for (int i = 0; i < 10; i++) {
std::cout << dis(gen) << " ";
}
return 0;
}Summary
To summurize, in modern C++, if we want to generate random numbers,
random_deviceis used to generate a random seed.mt19937is a random number generator.uniform_int_distribution,normal_distribution, anduniform_real_distributionare used to generate random numbers in a specific range or with a specific distribution.
Monte Carlo Simulation
The Basic Idea
Monte Carlo Simulation is a computational technique that uses random numbers to solve mathematical problems. 2
- Define a domain of possible inputs.
- Generate inputs randomly from the domain.
- Perform a deterministic computation on the inputs.
- Aggregate the results.
Example: Estimating Pi
The area of a unit circle is \(\pi\). The area of a unit square is 1.
If we randomly generate points in the unit square, the ratio of points that fall inside the unit circle to the total number of points is an estimate of \(\pi/1 = \pi\).
Bonimial tree
Consider a simple binomial model in which the stock price either goes up or down at the end of each period (step).
- Probability of going up: 55%
- Probability of going down: 45%
- Initial price P0 = $100
- Price change at each step: ±$10
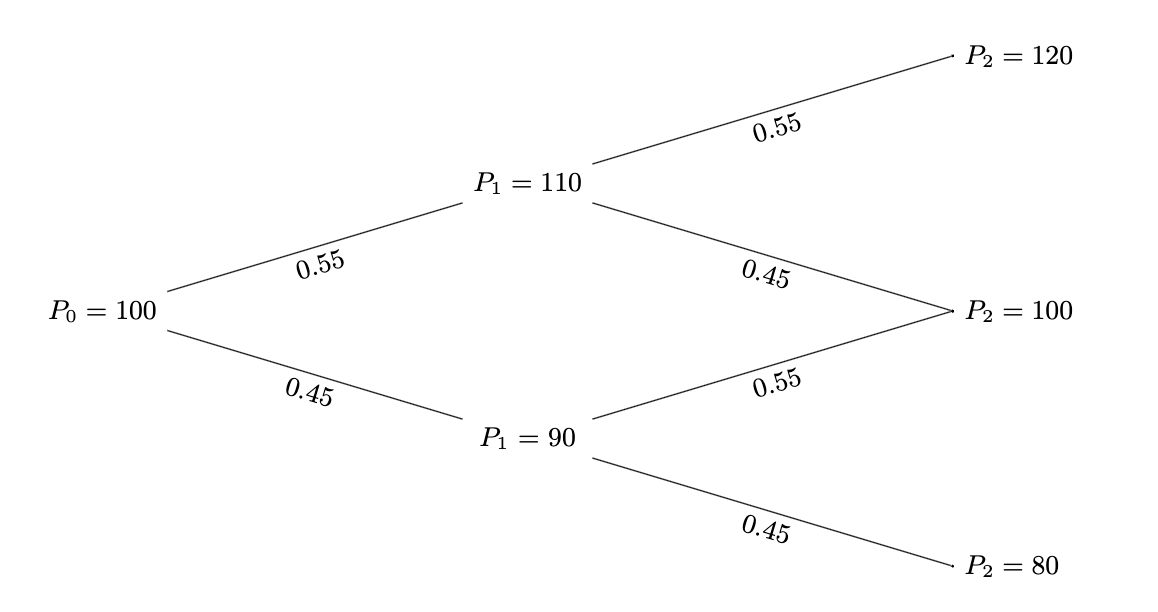
Estimate the stock price after 10 steps
We can simulate 10000 paths, each path has 10 steps.
- For each path, we simulate the stock price at each step.
- Draw a uniform random number between 0 and 1.
- If the number is less than 0.55, the stock price goes up by $10.
- Otherwise, the stock price goes down by $10.
- The final stock price of each path is the stock price at the end of the 10th step.
- We average the final stock prices of all paths to get the estimated stock price after 10 steps.